数据结构
三大结构
- 不受限制
- 链表
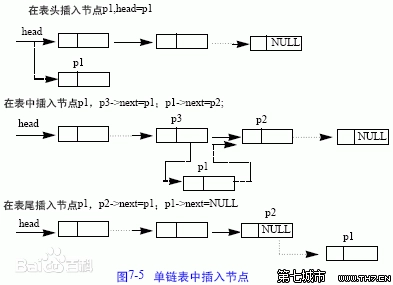
- 单向链表
- 双向链表
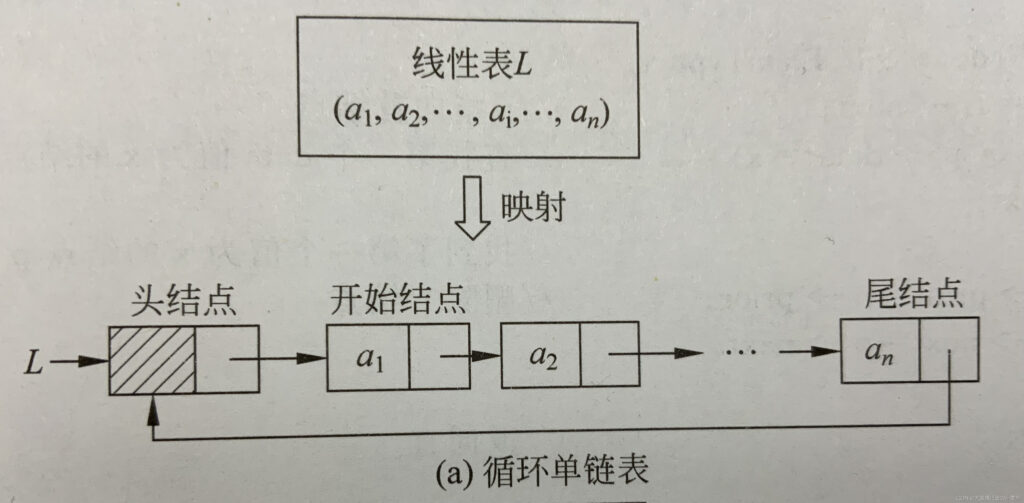
- 循环链表
- 头节点可装数可不装数
- 连不连续均可
- 相关图片👇


- 顺表
- O(1)时间复杂度
- 可用地址查询
- 元素地址数组名+下标
- 链表
- 受限制
- 树
- 图
栈
stack<int> s;
s.push(__) = s[++top]=__
s.size() = top
s.pop() = top--
s.empty = top==-1
s.top() = s[top]
前中后缀表达式
易考转换
样例代码《海港》
题目背景
NOIP2016 普及组 T3
题目描述
小 K 是一个海港的海关工作人员,每天都有许多船只到达海港,船上通常有很多来自不同国家的乘客。
小 K 对这些到达海港的船只非常感兴趣,他按照时间记录下了到达海港的每一艘船只情况;对于第 i 艘到达的船,他记录了这艘船到达的时间 ti (单位:秒),船上的乘客数 ki,以及每名乘客的国籍 xi,1,xi,2,…,xi,k。
小K统计了 n 艘船的信息,希望你帮忙计算出以每一艘船到达时间为止的 24 小时(24 小时 =86400 秒)内所有乘船到达的乘客来自多少个不同的国家。
形式化地讲,你需要计算 n 条信息。对于输出的第 i 条信息,你需要统计满足 ti−86400<tp≤ti 的船只 p,在所有的 xp,j 中,总共有多少个不同的数。
输入格式
第一行输入一个正整数 n,表示小 K 统计了 n 艘船的信息。
接下来 n 行,每行描述一艘船的信息:前两个整数 ti 和 ki 分别表示这艘船到达海港的时间和船上的乘客数量,接下来 ki 个整数 xi,j 表示船上乘客的国籍。
保证输入的 ti 是递增的,单位是秒;表示从小K第一次上班开始计时,这艘船在第 ti 秒到达海港。
保证 1≤n≤105,∑ki≤3×105 ,1≤xi,j≤105, 1≤ti−1≤ti≤109。
其中 ∑ki 表示所有的 ki 的和。
输出格式
输出 n 行,第 i 行输出一个整数表示第 i 艘船到达后的统计信息。
输入输出样例
输入 #1
3 1 4 4 1 2 2 2 2 2 3 10 1 3
输出 #1
3 4 4
输入 #2
4 1 4 1 2 2 3 3 2 2 3 86401 2 3 4 86402 1 5
输出 #2
3 3 3 4
说明/提示
【样例解释 1】
第一艘船在第 1 秒到达海港,最近 24 小时到达的船是第一艘船,共有 4 个乘客,分别是来自国家 4,1,2,2,共来自 3 个不同的国家;
第二艘船在第 2 秒到达海港,最近 24 小时到达的船是第一艘船和第二艘船,共有 4+2=6 个乘客,分别是来自国家 4,1,2,2,2,3,共来自 4 个不同的国家;
第三艘船在第 10 秒到达海港,最近 24 小时到达的船是第一艘船、第二艘船和第三艘船,共有 4+2+1=7 个乘客,分别是来自国家 4,1,2,2,2,3,3,共来自 4 个不同的国家。
【样例解释 2】
第一艘船在第 1 秒到达海港,最近 24 小时到达的船是第一艘船,共有 4 个乘客,分别是来自国家 1,2,2,3,共来自 3 个不同的国家。
第二艘船在第 3 秒到达海港,最近 24 小时到达的船是第一艘船和第二艘船,共有 4+2=6 个乘客,分别是来自国家 1,2,2,3,2,3,共来自 3 个不同的国家。
第三艘船在第 86401 秒到达海港,最近 24 小时到达的船是第二艘船和第三艘船,共有 2+2=4 个乘客,分别是来自国家 2,3,3,4,共来自 3 个不同的国家。
第四艘船在第 86402 秒到达海港,最近 24 小时到达的船是第二艘船、第三艘船和第四艘船,共有 2+2+1=5 个乘客,分别是来自国家 2,3,3,4,5,共来自 4个 不同的国家。
【数据范围】
- 对于 10% 的测试点,n=1,∑ki≤10,1≤xi,j≤10,1≤ti≤10。
- 对于 20% 的测试点,1≤n≤10,∑ki≤100,1≤xi,j≤100,1≤ti≤32767。
- 对于 40% 的测试点,1≤n≤100,∑ki≤100,1≤xi,j≤100,1≤ti≤86400。
- 对于 70% 的测试点,1≤n≤1000,∑ki≤3000,1≤xi,j≤1000,1≤ti≤109。
- 对于 100% 的测试点,1≤n≤105,∑ki≤3×105,1≤xi,j≤105,1≤ti≤109。
#include <bits/stdc++.h>
using namespace std;
struct person {
int time;
int nation;
} q[300006];
int f, r, ans, b[100086];
int n, t, k, x;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> t >> k;
for (int j = 1; j <= k; j++) {
cin >> x;
q[r].time = t;
q[r].nation = x;
r++;
b[x]++;
if (b[x] == 1) {
ans++;
}
}
while (f < r) {
if (t - q[f].time >= 86400) {
b[q[f].nation]--;
if (b[q[f].nation] == 0) {
ans--;
}
f++;
} else {
break;
}
}
cout << ans << endl;
}
return 0;
}T498818 [NOIP2000 普及组] 计算器的改良
题目背景
NCL 是一家专门从事计算器改良与升级的实验室,最近该实验室收到了某公司所委托的一个任务:需要在该公司某型号的计算器上加上解一元一次方程的功能。实验室将这个任务交给了一个刚进入的新手 ZL 先生。
题目描述
为了很好的完成这个任务,ZL 先生首先研究了一些一元一次方程的实例:
- 4+3x=8。
- 6a−5+1=2−2a。
- −5+12y=0。
ZL 先生被主管告之,在计算器上键入的一个一元一次方程中,只包含整数、小写字母及 +、-、= 这三个数学符号(当然,符号“-”既可作减号,也可作负号)。方程中并没有括号,也没有除号,方程中的字母表示未知数。
你可假设对键入的方程的正确性的判断是由另一个程序员在做,或者说可认为键入的一元一次方程均为合法的,且有唯一实数解。
输入格式
一个一元一次方程。
输出格式
解方程的结果(精确至小数点后三位)。
输入输出样例
6a-5+1=2-2a
a=0.750
#include<bits/stdc++.h>
using namespace std;
string s;
int fuhao=1;
int zuoyou=1;
int num=0;
float k,b;
char x;
int main(){
cin>>s;
s+="+";
int len=s.size();
for(int i=0;i<len;i++){
if(s[i]=='+'){
b+=num*fuhao*zuoyou;
fuhao=1;
num=0;
}else if(s[i]=='-'){
b+=num*fuhao*zuoyou;
num=0;
fuhao=-1;
}else if(s[i]=='='){
b+=num*fuhao*zuoyou;
num=0;
fuhao=1;
zuoyou=-1;
}else if(s[i]>='0'&&s[i]<='9'){
num=num*10+(s[i]-'0');
}else{
if(!num){
num=1;
}
k+=num*fuhao*zuoyou;
x=s[i];
num=0;
fuhao=1;
}
}
float ans=(-b)*1.0/k;
cout<<x<<"=";
printf("%.3lf",ans);
return 0;
}数学基础
an-bn
an-bn=(a-b)(an-1b0+an-2b1+···+a0bn-1)
如果一个数的每一位都能被n整除,那么这个数就能被n整除



暂无评论内容