【2】初赛备赛-谷穗社区

集合

确定性、无序性、相异性

集合装的事务叫元素

所有实数集合用 R 表示

所有整数用Z 表示

所有正整数用 Z⁺ 表示

所有自然数用N表示（自然数包含0）

所有有理数集用Q表示

表示

集合里的元素用大括号表示

{1，5，7，-2，9}

空集合

{}

空集合的符号是‌∅‌，‌这是一个倒转的大写希腊字母φ。‌这个符号由法国数学家尼古拉·布尔巴基于20世纪30年代引入，‌并被广泛应用于集合论和其他数学领域。‌

在数学中，‌空集是一个不包含任何元素的集合，‌具有独特的性质和广泛的应用。‌例如，‌空集是任何集合的子集，‌是任何非空集合的真子集。‌

请注意，‌在某些情况下，‌空集也可能用符号Ø来表示，‌但这并不是最普遍或标准的表示方法。‌在大多数情况下，‌推荐使用∅来表示空集。‌

韦恩图

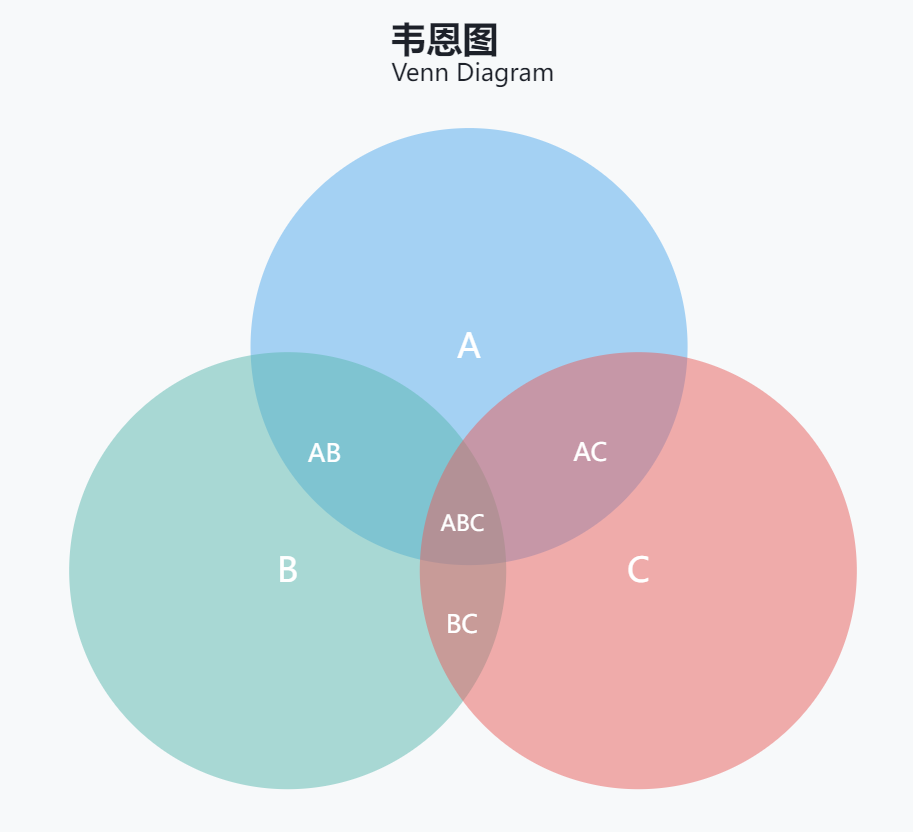
用描述性的语言描述集合

{x|1<x<2}

符号

版本一

符号l	意思	例子
{ }	集合：收集起来的元素	{1,2,3,4}
A ∪ B	并集: 在 A 或/和 B 里（在两个或任何一个集里）	C ∪ D = {1,2,3,4,5}
A ∩ B	交集: 在 A 和 B 里（不能只在一个集里）	C ∩ D = {3,4}
A ⊆ B	子集：A 含有 B 的一些（或所有）元素	{3,4,5} ⊆ D
A ⊂ B	真子集：A 含有 B 的一些元素	{3,5} ⊂ D
A ⊄ B	非子集：A 不是 B 的子集	{1,6} ⊄ C
A ⊇ B	超集：A 有 B 的所有元素，或更多	{1,2,3} ⊇ {1,2,3}
A ⊃ B	真超集：A 有 B 的所有元素及更多	{1,2,3,4} ⊃ {1,2,3}
A ⊅ B	非超集：A 不是 B 的超集	{1,2,6} ⊅ {1,9}
A^c	补集（也称余集）：不在 A 的元素	D^c = {1,2,6,7} 当 = {1,2,3,4,5,6,7}
A − B	差集：在 A 里但不在 B 里	{1,2,3,4} − {3,4} = {1,2}
a ∈ A	是…的元素：a 是 A 的元素	3 ∈ {1,2,3,4}
b ∉ A	不是…的元素：b 不是 A 的元素	6 ∉ {1,2,3,4}
∅	空集 = {}	{1,2} ∩ {3,4} = Ø
	全集：含有所有可能的元素的集（在当前话题中）

P(A)	幂集：A 的所有子集	P({1,2}) = { {}, {1}, {2}, {1,2} }
A = B	相等：有相同的元素	{3,4,5} = {3,4,5}
A×B	笛卡尓积：第一个对象是A的成员而第二个对象是B的成员的所有可能有序对的集	{1,2} × {3,4} = {(1,3), (1,4), (2,3), (2,4)}
\|A\|	基数：集 A 的元素的个数	\|{3,4}\| = 2

\|	使得	{ n \| n > 0 } = {1,2,3,…}
:	使得	{ n : n > 0 } = {1,2,3,…}
∀	对于所有	∀x>1, x²>x
∃	存在	∃ x \| x²>x
∴	因此	a=b ∴ b=a

	自然数	{1,2,3,…} 或 {0,1,2,3,…}
	整数	{…, -3, -2, -1, 0, 1, 2, 3, …}
	有理数
	代数数
	实数
	虚数	3i
	复数	2 + 5i

版本二

符号	符号名称	含义/ 定义	例
{}	设置	元素集合	A = {3,7,9,14}， B = {9,14,28}
\|	这样	以便	A = { x \| X ∈ $\ mathbb {R}$ ，X <0}
⋂	路口	属于集合A和集合B的对象	A⋂B = {9,14}
⋃	联盟	属于集合A或集合B的对象	A⋃B = {3,7,9,14,28}
⊆	子集	A是B的子集。集合A包含在集合B中。	{9,14,28}⊆{9,14,28}
⊂	适当子集/严格子集	A是B的子集，但A不等于B。	{9,14}⊂{9,14,28}
⊄	不是子集	集A不是集B的子集	{9,66}⊄{9,14,28}
⊇	超集	A是B的超集。集合A包括集合B	{9,14,28}⊇{9,14,28}
⊃	适当的超集/严格的超集	A是B的超集，但B不等于A。	{9,14,28}⊃{9,14}
⊅	不超集	集A不是集B的超集	{9,14,28}⊅{9,66}
2^一	功率设定	A的所有子集
$\ mathcal {P}（A）$	功率设定	A的所有子集
A = B	平等	两组都有相同的成员	A = {3,9,14}， B = {3,9,14}， A = B
一^ç	补充	所有不属于集合A的对象
一种’	补充	所有不属于集合A的对象
A \ B	相对互补	属于A而不属于B的对象	A = {3,9,14}， B = {1,2,3}， A \ B = {9,14}
AB	相对互补	属于A而不属于B的对象	A = {3,9,14}， B = {1,2,3}， A-B = {9,14}
A∆B	对称差异	属于A或B但不属于它们的交集的对象	A = {3,9,14}， B = {1,2,3}， A ∆ B = {1,2,9,14}
⊖	对称差异	属于A或B但不属于它们的交集的对象	A = {3,9,14}， B = {1,2,3}， A = B = {1,2,9,14}
一∈A	的元素，属于	设定会员	A = {3,9,14}，3∈A
X ∉A	不是元素	没有固定的会员资格	A = {3,9,14}，1∉A
（a，b）	有序对	2个元素的集合
A×B	笛卡尔积	A和B中所有有序对的集合
\| A \|	基数	集A的元素数	A = {3,9,14}，\| A \| = 3
＃一种	基数	集A的元素数	A = {3,9,14}，＃A = 3
\|	竖线	这样	A = {x \| 3 <x <14}
ℵ ₀	空	自然数的无限基数
ℵ ₁	炔属	可数序数集的基数
Ø	空集	Ø= {}	A =Ø
$\ mathbb {U}$	通用集	所有可能值的集合
ℕ ₀	自然数/整数集（零）	$\ mathbb {N}$ ₀ = {0,1,2,3,4，…}	0∈ $\ mathbb {N}$ ₀
ℕ ₁	自然数/整数集（不包含零）	$\ mathbb {N}$ ₁ = {1,2,3,4,5，…}	6∈ $\ mathbb {N}$ ₁
ℤ	整数集	$\ mathbb {Z}$ = {…- 3，-2，-1,0,1,2,3，…}	-6∈ $\ mathbb {Z}$
ℚ	有理数集	$\ mathbb {Q}$ = { x \| X =一个/ b，一个，b ∈ $\ mathbb {Z}$ 和b ≠0}	2/6∈ $\ mathbb {Q}$
ℝ	实数集	$\ mathbb {R}$ = { x \| -∞< x <∞}	6.343434∈ $\ mathbb {R}$
ℂ	复数集	$\ mathbb {C}$ = { z \| z = a + bi，-∞< a <∞，-∞< b <∞}	6 + 2我∈ $\ mathbb {C}$

输入输出解绑

ios::sync_with_stdio(false);
cin.tie(0);

文章版权归作者所有，未经允许请勿转载。

THE END

C++代码随笔